Dans l’arsenal du data scientist, certains outils traversent les époques sans prendre une ride. La régression linéaire est l’un d’entre eux. Bien qu’elle soit l’une des techniques les plus anciennes de l’analyse statistique, elle reste aujourd’hui le socle sur lequel repose une immense partie de l’intelligence artificielle moderne. Que ce soit pour prédire le prix d’un bien immobilier ou anticiper les ventes d’une entreprise, ce modèle mathématique offre une clarté et une interprétabilité que les algorithmes de “boîte noire” plus complexes peinent parfois à égaler.
Comprendre la régression linéaire, c’est apprendre à lire les relations cachées entre les phénomènes. C’est transformer une nuée de points apparemment désordonnés en une tendance claire et exploitable. Pour un débutant en informatique ou un passionné de tech, maîtriser ce concept n’est pas seulement une étape académique, c’est l’acquisition d’une lunette astronomique permettant d’observer les données avec une précision chirurgicale, afin d’en extraire des prévisions fiables et rigoureuses.
1. Comment fonctionne concrètement la régression linéaire et dans quels cas l’utiliser ?
L’une des premières interrogations de l’utilisateur novice concerne la mécanique interne de cet outil. Comment une simple droite peut-elle prédire l’avenir ? La régression linéaire repose sur l’idée que si deux variables sont liées (par exemple, la surface d’un appartement et son prix), on peut modéliser cette relation par une fonction mathématique. L’objectif est de trouver la ligne droite qui passe “le plus près possible” de l’ensemble des données historiques pour ensuite prolonger cette ligne vers l’inconnu.
L’utilité actuelle de cette méthode est omniprésente. Dans le secteur financier, elle sert à évaluer les risques de crédit. Dans le marketing, elle aide à déterminer l’impact d’une hausse de budget publicitaire sur le chiffre d’affaires. Sa force réside dans sa simplicité : elle ne se contente pas de donner un résultat, elle explique comment chaque facteur influence la réponse finale. C’est cette transparence qui en fait un outil de décision privilégié pour les dirigeants et les analystes.
2. Définition et fondements techniques du concept
Une définition simple pour tous
Imaginez que vous observez la croissance d’une plante. Vous remarquez que plus vous donnez d’eau (dans une certaine limite), plus elle grandit. La régression linéaire, c’est la règle de trois améliorée qui vous permet de dire : “Si je donne 10 ml d’eau de plus, la plante gagnera probablement 2 cm”. C’est l’art de tracer une route droite au milieu d’un champ de données pour voir où elle mène.
Les fondements techniques et mathématiques
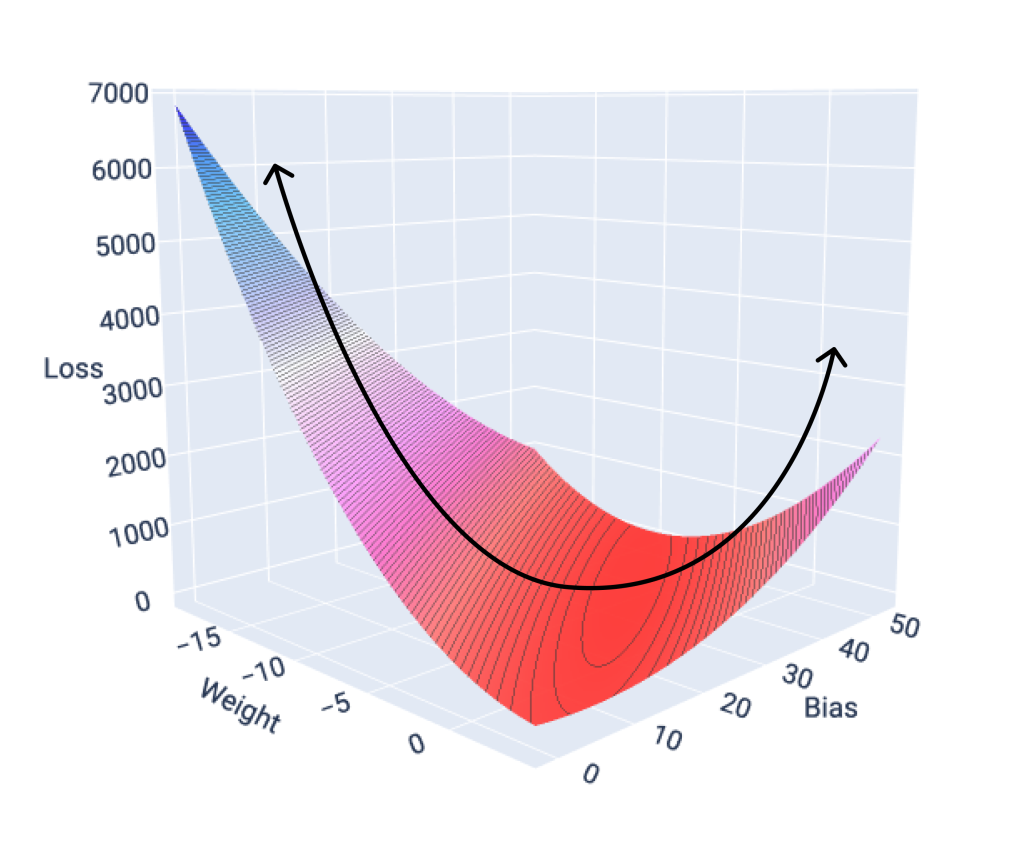
Techniquement, ce modèle cherche à établir une équation de type $y = ax + b$. Ici, $y$ représente la variable que l’on veut prédire (la variable dépendante), $x$ est la variable explicative (indépendante), $a$ est la pente de la droite (le coefficient) et $b$ est l’ordonnée à l’origine. L’enjeu est de minimiser la distance entre les points réels et la droite, une méthode souvent appelée “moindres carrés ordinaires”.
La structure de cet algorithme s’appuie sur des concepts d’algèbre linéaire et de statistiques, discipline dont elle est issue. Elle nécessite que certaines conditions soient remplies pour être fiable, comme la linéarité de la relation et l’indépendance des erreurs. Bien que cela puisse paraître complexe, les logiciels modernes comme Python ou R effectuent ces calculs en une fraction de seconde, laissant à l’humain la tâche cruciale de l’interprétation des coefficients.
3. Les différents types de modèles de régression
La régression linéaire simple
C’est la forme la plus élémentaire. On utilise une seule variable $x$ pour prédire $y$. Par exemple, prédire la consommation de carburant d’une voiture uniquement en fonction de son poids. C’est l’outil idéal pour débuter et comprendre comment une variable influe directement sur une autre sans bruit parasite complexe.
La régression linéaire multiple
Dans la réalité, un phénomène est rarement causé par un seul facteur. La régression multiple permet d’ajouter autant de variables explicatives que nécessaire ($x1, x2, x3…$). Pour reprendre l’exemple de l’immobilier, on ne regarde plus seulement la surface, mais aussi le nombre de chambres, le quartier et l’année de construction. Le modèle devient alors un outil multidimensionnel puissant.
Régression polynomiale et régularisation
Parfois, la relation n’est pas une ligne droite parfaite mais une courbe. On utilise alors des variantes polynomiales. De plus, pour éviter que le modèle ne devienne “trop complexe” et ne fasse des erreurs sur de nouvelles données (un phénomène appelé surapprentissage), on utilise des techniques de régularisation comme les méthodes Ridge ou Lasso, qui simplifient mathématiquement l’équation.
4. À quoi sert ce domaine et quel est l’impact du métier d’analyste ?
La prédiction au service de l’entreprise
Le métier de data analyst ou de statisticien consiste en grande partie à construire ces modèles. Dans la logistique, cela sert à prévoir le temps de livraison en fonction de la distance et du trafic. L’impact est direct : une meilleure prédiction permet d’optimiser les stocks, de réduire les coûts et d’améliorer la satisfaction client. L’analyste est celui qui traduit la réalité en équations exploitables.
L’évaluation de l’impact des politiques publiques
Au-delà de l’aspect commercial, la régression est un outil social. Les économistes l’utilisent pour mesurer l’efficacité d’une nouvelle loi. Par exemple, quel a été l’impact réel de l’augmentation du prix du tabac sur la consommation ? En contrôlant d’autres variables (revenu, âge), la régression permet d’isoler l’effet précis d’une décision politique, offrant ainsi une base scientifique au débat public.
L’ingénierie et la maintenance prédictive
Dans l’industrie, on utilise ces modèles pour surveiller l’usure des machines. En analysant la température et la vibration au fil du temps, une régression peut signaler qu’une pièce va probablement casser dans les 48 heures. Cela permet d’intervenir avant la panne, économisant des sommes astronomiques et garantissant la sécurité des opérateurs sur le terrain.
5. Comment construire un modèle de régression linéaire fiable ?
La collecte et la préparation des données
Avant de lancer un calcul, il faut des données saines. Cela implique de traiter les valeurs manquantes et de supprimer les “outliers” (données aberrantes) qui pourraient fausser la pente de la droite. Une seule donnée erronée peut parfois tirer toute la droite vers le haut ou le bas, rendant les prédictions totalement inutilisables.
Le choix des variables (Feature Selection)
Mettre toutes les données disponibles dans le modèle n’est pas une bonne stratégie. Il faut choisir les variables qui ont réellement un lien logique avec le résultat. L’analyste doit faire preuve de discernement pour ne pas corréler des éléments qui n’ont rien à voir entre eux, évitant ainsi de tomber dans le piège des corrélations illusoires.
L’évaluation de la performance
Une fois la droite tracée, comment savoir si elle est bonne ? On utilise des indicateurs comme le $R^2$ (coefficient de détermination), qui indique quel pourcentage de la variation des données est expliqué par le modèle. On vérifie également l’erreur quadratique moyenne (MSE) pour mesurer l’écart moyen entre les prédictions et la réalité. Un bon modèle est un modèle qui se trompe le moins possible.
6. Applications concrètes : la régression dans notre vie quotidienne
Le calcul des primes d’assurance
Lorsque vous souscrivez à une assurance auto, votre prime est calculée via une régression. Les assureurs croisent votre âge, votre historique de conduite et la puissance de votre véhicule pour estimer votre coût probable en cas d’accident. C’est la régression qui fixe le prix juste, permettant à l’assureur d’équilibrer ses comptes tout en restant compétitif.
La météo et les sciences environnementales
Bien que les modèles météo soient aujourd’hui extrêmement complexes, ils intègrent souvent des régressions linéaires pour corriger les prévisions locales. En comparant les prévisions brutes avec les températures réellement observées sur une station donnée au cours des années précédentes, le système apprend à corriger ses propres erreurs de manière linéaire.
Le sport de haut niveau et les performances
Dans le football ou le basketball, les analystes utilisent la régression pour évaluer la valeur réelle d’un joueur. On peut prédire le nombre de buts qu’un attaquant devrait marquer en fonction de la qualité des passes qu’il reçoit. Si un joueur marque plus que ce que la régression prévoit, il est considéré comme exceptionnellement efficace. C’est l’essence même du “Moneyball”.
7. Clarification des idées reçues et limites du modèle
“Corrélation n’est pas causalité”
C’est le piège numéro un. Si une régression montre que les ventes de glaces augmentent en même temps que les coups de soleil, cela ne veut pas dire que manger des glaces provoque des brûlures. Il y a une variable cachée : le soleil. La régression montre une relation mathématique, mais c’est à l’humain de valider le lien logique et la cause réelle derrière les chiffres.
Le problème de la non-linéarité
Toutes les relations dans le monde ne sont pas des lignes droites. Si vous essayez d’utiliser une régression linéaire pour modéliser un phénomène qui explose de façon exponentielle (comme la propagation d’un virus), vos prédictions seront dramatiquement fausses. Il est crucial de visualiser ses données avant de choisir ce modèle pour s’assurer qu’une droite est bien appropriée.
La sensibilité aux valeurs aberrantes
La régression linéaire est “fragile” face aux points extrêmes. Si vous étudiez le salaire moyen d’un quartier et que le milliardaire local s’invite dans votre jeu de données, votre droite va s’envoler, masquant la réalité de tous les autres habitants. L’analyste doit donc toujours vérifier la distribution de ses données avant de faire confiance aveuglément à ses coefficients.
8. L’avenir de la régression et les tendances technologiques
L’avenir de la régression ne réside pas dans sa disparition, mais dans son intégration. Elle est désormais la brique de base de l’AutoML (Machine Learning Automatisé). Les systèmes modernes testent automatiquement des régressions linéaires avant d’essayer des modèles plus lourds, car si une simple droite suffit, elle sera toujours préférée pour sa rapidité et son coût énergétique réduit.
Une autre tendance forte est l’IA explicable (XAI). Face à la montée en puissance des algorithmes opaques, la régression linéaire revient en grâce car elle est “auditable” par nature. Dans les secteurs régulés comme la santé ou la justice, il est légalement obligatoire de pouvoir expliquer pourquoi une décision a été prise. La régression offre cette garantie, car on peut pointer du doigt le coefficient exact qui a influencé le résultat.
Enfin, l’évolution vers le calcul distribué permet de calculer des régressions sur des milliards de lignes en quelques secondes. Ce qui prenait des jours à un ordinateur des années 80 est désormais instantané grâce au Cloud. La régression linéaire devient ainsi un outil de monitoring en temps réel, capable d’ajuster des prix ou des flux logistiques à la microseconde, prouvant que même les vieux outils peuvent être à la pointe de la modernité
Conclusion
La régression linéaire est bien plus qu’une simple formule mathématique ; c’est un langage universel pour décoder les relations entre les variables qui régissent notre monde. Sa simplicité est sa plus grande force, offrant une porte d’entrée accessible et pourtant incroyablement robuste vers la science des données. En apprenant à maîtriser ce modèle, vous ne vous contentez pas de tracer des droites : vous apprenez à structurer votre pensée pour séparer le signal du bruit, une compétence vitale dans notre ère de l’information.
Vous souhaitez vous former au Big Data ? Retrouvez les formations Data Scientist & AI Engineer et Data Analyst qui vous forment aux métiers de Data Analyst, Data Scientist, Data Engineer et AI Scientist.
Merci pour votre lecture ! Si vous souhaitez lire nos prochains articles autour de la Data et de l’IA, vous pouvez nous suivre sur Facebook, LinkedIn et Twitter pour être notifié lorsqu’un nouvel article est publié !